III-1-(1) 密度汎関数法とその展開

物質は原子から構成されています。原子は原子核と電子からできています。原子の大きさは約0.1ナノメートルです。そこでの電子の振舞いは量子論によって記述されます。量子論によれば、電子は粒子であると同時に波動でもあります。物質内では、電子の波動性や粒子性が見え隠れして、豊かな自然現象が見られます。

したがって、物質を舞台とする現象を理論的に解明し、さらにはそれに基づいて新しい現象の予言や、物質のデザインをするためには、量子論に立脚した計算手法が必要となります。粒子性と波動性の記述のために、電子の波動関数というものが導入されます。その波動関数は、原理的には、多くの電子に対するSchroedinger方程式あるいはDirac方程式を解けば求められます。ですがそれは実際上は不可能です。電子同士の相互作用の取り扱い方が難しいからです。こうした取り扱いの問題は、多体問題とよばれます。

Schroedinger方程式は、エネルギーを波動関数空間の様々な波動関数について変分した方程式とみなすこともできます。HohenbergとKohnが編み出した密度汎関数理論では、エネルギーは波動関数の汎関数ではなく、１電子密度の汎関数であることが厳密に証明されました。それにより、Schroedinger方程式ではなく、エネルギーを１電子密度で変分した変分方程式（Kohn-Sham方程式とよばれます）を解けばよいということになります。これにより問題は非常に簡単化されました。

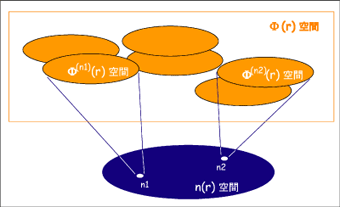[図：密度汎関数理論の概念。物質のエネルギーは１電子密度の汎関数である。]

実際1980年代以降、密度汎関数理論は様々な物質に適用され大きな成功をおさめました。大抵の物質の構造的および電子的性質は、密度汎関数理論により、十分定量的に記述されます。

近年、生体分子やナノ構造体といった、原子数で千以上からなる系に大きな関心がよせられるようになり、それに応じて、これまで比較的小さい系で、物性の定量的記述に成功を収めてきた密度汎関数法に基づく第一原理計算手法をこれら大規模系に適用し、原子・電子構造の定量的記述、あるいは新奇物性の機能予測を行うという動きが活発化しています。

当研究室では、実空間有限差分法およびノルム保存擬ポテンシャル法による第一原理電子状態計算コードの開発を行い、さらに実空間法の特性を活かした並列計算コードの開発も同時に行い、これによって1000原子～10000原子からなる系の第一原理計算を目指しています。

実空間法では３次元空間（ユニットセル）を離散的な格子で記述します。波動関数その他の量は各格子点上での値で表現し、運動エネルギー演算子のラプラシアンは高次有限差分で評価します。非局所擬ポテンシャルは本来実空間表示では有限レンジであり、実空間法ではその特性を直接利用することができ、これは非局所擬ポテンシャルの演算量をO(N3)からO(N2)に減らすことにつながります。また実空間法では、従来の平面波展開を用いる手法と異なり、ハミルトニアンの演算の際に高速フーリエ変換を用いる必要がなく、これによって並列化に非常に適したアルゴリズムを与えることができます[Journal of Computational Physics: 229, 2339 (2010)]。

またコンダクタンスやキャパシタンスといったナノ構造において重要な物理量の計算も大きなターゲットです。密度汎関数理論をベースとした、そうした計算手法の開発も進んでいます。[Physical Review B 69, 045401 (2004)]

電子同士の量子論的な相互作用が大変強い物質群を強相関系とよぶことがあります。現在の密度汎関数理論では、そうした物質群を定量的には記述できていません。新計算手法の開拓が必要です。いわゆる強相関系ではありませんが、バイオ物質の構造決定に重要な、ヴァン・デア・ワールス力を記述することも重要です。ヴァン・デア・ワールス力は誘起双極子同士の相互作用なので、電子相関の問題ととらえられます。その記述法は、当グループでの緊急の課題です。